What Is a Multinomial Retrogression Projection (MRP)?
MRP is a statistical method often used when there exists a relationship between multiple variables that can be effectively characterized by a multinomial equation.
In trading and technical analysis, multinomial retrogression can be used in discerning the underlying trends in asset prices and identifying support and resistance levels. For instance, linear retrogression or linear regression, a common form of multinomial retrogression with a degree of 1, is often utilized for this purpose, providing insights into the linear trend of price movements over time.
The application of multinomial retrogression for projection purposes becomes useful when we hypothesize that the fundamental trend of a specific asset conforms to a multinomial equation of a designated degree, and we presume that this hypothesis remains valid for subsequent time periods (t+1, t+2, …, t+n). Although this assumption rarely mirrors reality with complete accuracy, it can be effective when engaged in long-term evaluations of assets like Bitcoin, where identifying sustained trends is critical amidst market volatility.
Finding the multinomial degree is typically guided by the nature of the observed trend. In other words, it is uncommon to exceed a degree of 3, as higher degrees have a tendency to accentuate the noisy fluctuations in the data. Therefore, selecting an appropriate degree ensures that the multinomial retrogression model effectively captures the underlying trend without being overly influenced by extraneous factors.
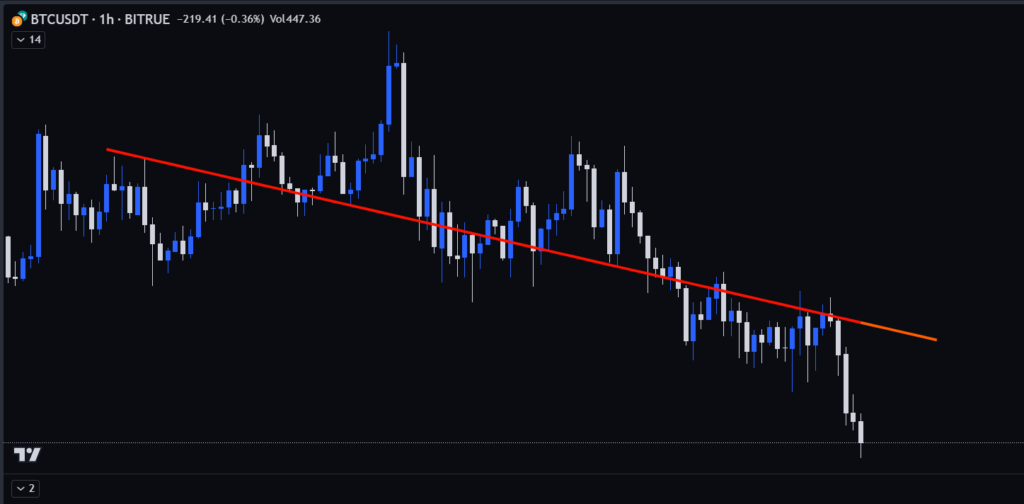
Image 1: Utilizing a length or period of 100 and a multinomial degree of 1
Using a multinomial of degree 1 will return a line, and as such can be considered when the underlying trend is linear. We can improve the fit by using a higher degree.
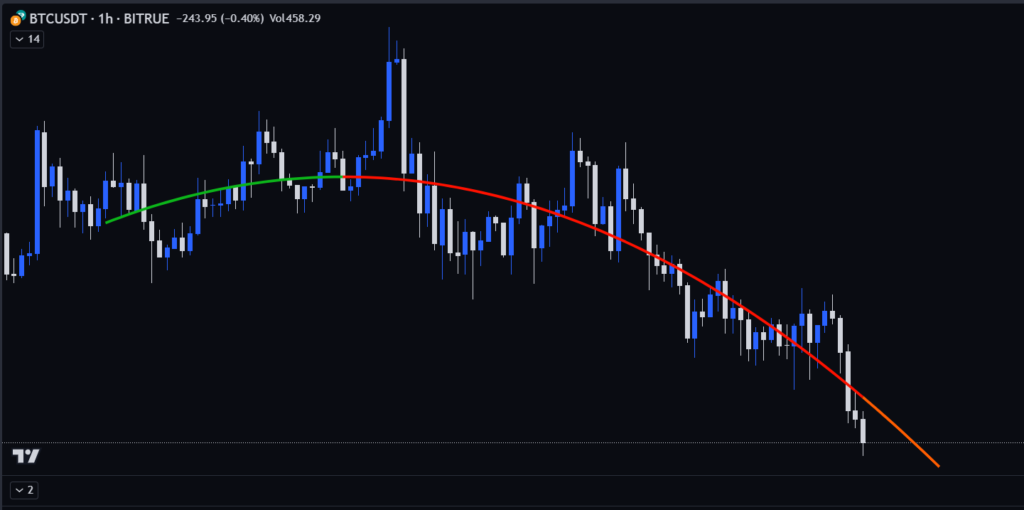
Image 2: Utilizing a length or period of 100 and a multinomial degree of 2
A multinomial of degree 2, will model more parabolic observations. And so on.
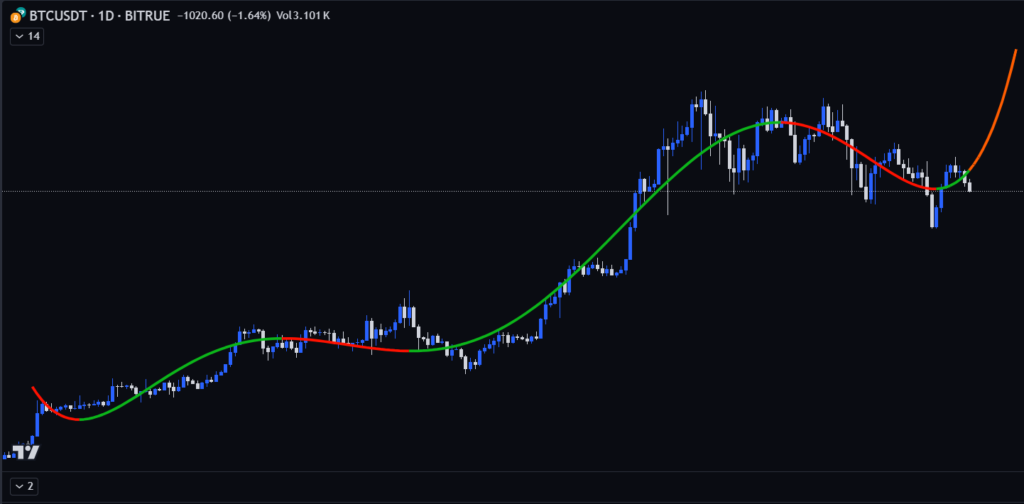
Image 3: Utilizing a length or period of 200 and a multinomial degree of 6
Thus, the projection of higher degree multinomials can eventually highlight future turning points due to the nature of the multinomial, however there are no guarantee that these will reflect exact future reversals.
How Is a Multinomial Retrogression Projection Calculated
A multinomial retrogression model y(t) of degree p is described by:
y(t) = β(0) + β(1)x(t) + β(2)x(t)^2 + … + β(p)x(t)^p
The vector coefficients β are obtained where the sum of the squared error between the observations and y(t) is minimized. This can be achieved through directly solving a system of equations:
β(0) + β(1)x(0) + β(2)x(0)^2 + … + β(p)x(0)^p = y(0)
β(0) + β(1)x(1) + β(2)x(1)^2 + … + β(p)x(1)^p = y(1)
…
β(0) + β(1)x(t-1) + β(2)x(t-1)^2 + … + β(p)x(t-1)^p = y(t-1)
[/list]
Note that solving this system of equations for higher degrees [i]p[/i] with high [i]x[/i] values can drastically affect the accuracy of the results. One method to avoid this can be to subtract [i]x[/i] by its mean.
Why Use Multinomial Retrogression Projection – Some of the Benefits
- Flexibility: Multinomial regression can capture nonlinear relationships between variables, making it suitable for analyzing complex data patterns.
- Interpretability: Multinomial equations are relatively easy to understand.
- Versatility: This method can be applied to various types of data and variables beyond just financial markets.
Why Are Some Pitfalls of MRPs
- Overfitting: Higher-degree multinomial models may overfit the data, capturing noise rather than the underlying trend and leading to poor results.
- Sensitivity to Outliers: Multinomial regression can be sensitive to outliers in the data, impacting the accuracy of the predictions. These outliers are usually values that deviate from all other values in a data set, which may produce inaccurate results.
- Projection Risk: Projections or extrapolations beyond the observed data range assumes that historical trends will continue into the future, which do not always hold true, especially in volatile markets.
What Is Projection
Projection, sometimes referred to as extrapolation, is the process of estimating values beyond the range of known data points. In trading, it involves extending a trend or pattern into the future to predict potential outcomes.
How Is Projections Applied and Used
As explained in my other models, these methods vary depending on the underlying data and the desired forecast. Some common methods include linear, exponential, polynomial, and multinomial projections.
What are Some of the Benefits
- Forecasting: Provides insights into future trends and patterns, which helps in strategically planning the direction and move of the asset.
- Decision Making: Helps anticipate potential future scenarios, giving you an early chance to evaluate your position and next steps.
What are Some of Its Faults
- Assumptions: Projections assume that trends observed in the known data will continue into the future, which again are not always the case, particularly in volatile markets.
- Uncertainty: Predictions that are made become increasingly uncertain as they move further away from the observed data range, potentially leading to inaccurate forecasts.
- Risk of Error: Inaccurate projections can result in flawed predictions, especially if underlying factors change unexpectedly.
Now the Strategy: Multinomial Retrogression Projection Models
First, we collect historical data of the asset or variable being traded, then fit a multinomial curve to the historical data points using regression analysis. After which, we extend or project the multinomial curve beyond the observed data points to predict future price movements. Based on the projected predictions, we create a projected direction that the market or asset will move. Green being an upward move, red a downward move.
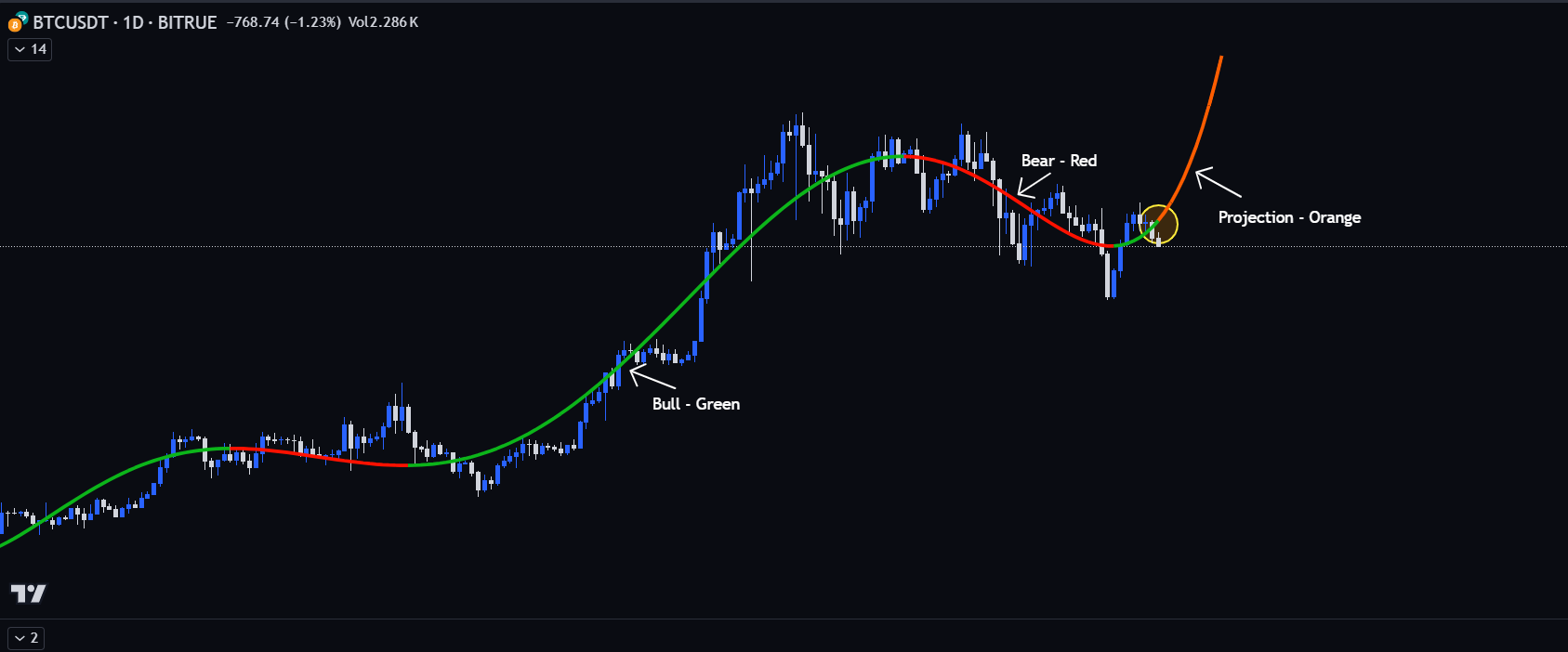
Now, let’s check out the code!
What Is Extrapolation
The second part of this strategy is utilizing extrapolations, or projections. In a nutshell, extrapolation is the process of estimating values beyond the range of known data points. In trading, it involves extending a trend or pattern into the future to predict potential outcomes.
